티스토리 뷰
컴퓨터에서 실수의 표현 (Fixed Point, Floating Point, Single Precision, Double Precision)
JG Ahn 2019. 11. 25. 21:50컴퓨터가 수를 표현하는 방식
사람들은 일반적으로 0~9의 조합을 가진 10진수를 사용하여 소통합니다.
하지만 컴퓨터는 0과 1의 조합으로 이루어진 비트만을 저장하고 연산할 수 있습니다.
따라서 컴퓨터에 저장되는 모든 것은 이진수로 저장됩니다.
실수의 표현 방식
컴퓨터에서 실수를 표현 하는 방법은 정수에 비해 훨씬 복잡합니다.
왜냐하면, 컴퓨터는 실수를 2진수로만 표현해야 하기 때문입니다.
따라서 실수를 표현하기 위해 다음과 같은 방식이 사용되고 있습니다.
1. 고정 소수점 (Fixed Point) 방식
2. 부동 소수점 (Floating Point) 방식
컴퓨터는 실수를 정확히 표현할 수 없다.
8.3 같은 실수를 2진수로 표현해 보면
8 => 1000(2)
0.3 => 0.01001100110011....(0011)의 무한 반복
이렇게 실수를 2진수로 표현할 때 표현하지 못하는 소수가 발생합니다.
어쩔 수 없이 컴퓨터에는 표현할 수 있는 가장 근사치의 값이 저장됩니다.
고정 소수점(Fixed Point) 방식
실수는 보통 정수부와 소수부로 나눌 수 있습니다
따라서 실수를 표현하는 가장 간단한 방식은 소수부의 자릿수를 정하여 , 고정된 자릿수의 소수를 표현하는 것이다.
32bit 실수를 고정 소수점 방식으로 표현하면 아래와 같습니다
하지만 이 방식은 정수부와 소수부의 자릿수가 크지 않으므로, 표현할 수 있는 값의 범위가 매우 적다는 단점이 있습니다.
정수를 표현하는 bit를 늘리면 큰 숫자를 표현할 수 있지만 정밀한 숫자를 표현하긴 힘듭니다.
또한 소수를 표현하는 bit를 늘릴 경우 정밀한 숫자를 표현할 수 있지만 큰 숫자를 표현하지 못합니다
이러한 문제를 해결하기 위해 소수점을 고정하지 않고 소수를 표현할 수 있는 부동 소수점(Floating Point)을 사용하고 있습니다.
|
부호(1bit) |
정수부(15bit) |
소수부(16bit) |
부동 소수점(Floating Point) 방식
현재 대부분의 시스템에서는 부동 소수점 방식으로 실수를 표현하고 있습니다.
고정 소수점 방식보다 넓은 범위의 수를 나타낼 수 있어 과학기술 계산에 많이 이용됩니다.
하지만 고정 소수점 방식보다 연산속도가 느려 별도의 전용 연상 장치를 두는 경우가 많습니다.
고정 소수점과 달리 정수 부분과 소수 부분의 자릿수가 일정하지 않으나, 유효 숫자의 자릿수는 정해져 있습니다.
부동 소수점 방식은 다음과 같은 수식을 이용하여 매우 큰 실수까지도 표현할 수 있습니다. (X=가수부, Y=지수부)

부동 소수점 방식은 하나의 실수를 부호(sign), 가수(mantissa), 지수(exponent)로 나누어 표현하는 방식입니다
부호는 전체 수가 양수 또는 음수를 표현하고,
지수는 2의 지수를 나타내며,
가수는 소수 이하를 표시합니다.
부동 소수점의 표현 범위에 따라
단점도(Single Precision), 배정도(Double Precision)로 나뉩니다
단정도 : 32bit float형 실수를 표준에 방식으로 표현하면 다음과 같습니다
배정도 : 64bit double형 실수는 지수부가 11bit, 가수부가 52bit로 바뀝니다.
|
부호(1bit) |
지수부(8bit) |
가수부(23bit) |
실수의 부호가 양수 일 때 부호 비트는 0,
음수 일 때는 1을 나타냅니다.
지수도 양수와 음수를 구별해서 나타낼 수 있어야 합니다.
양의 지수와 음의 지수를 표현하기 위해 바이어스(bias)를 사용합니다.
단정도 일때는 127, 배정도 일때는 1023을 사용합니다.
예를 들어,
2^10이라면 지수 10에 바이어스 127을 더한 137을 2진수로 바꾸어 지수에 저장하며,
2^-10이라면 지수 -10에 127을 더한 117을 2진수로 바꾸어 지수에 저장한다
가수에 저장된 데이터는 2진수를 정규화(Normalization)하여 나타냅니다.
예를 들어,
10진수 5를 나타낼 때 아래와 같이 나타낼 수 있는데
이 중에서 5의 정규화된 표현 방법은 5.0 * 10^0입니다.

부동 소수점 방식의 오차
부동 소수점 방식을 사용하면 고정 소수점 방식보다 훨씬 더 많은 범위까지 표현할 수 있습니다.
하지만 부동 소수점 방식에 의한 실수의 표현은 항상 오차가 존재한다는 단점을 가지고 있습니다.

문제 1)
8.625를 단정도(Single Precision) 방식으로 표현하라.
풀이)
1. 실수를 이진수로 표현합니다.

2. 가수를 정규화합니다.
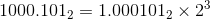
3. 지수(exponent)를 찾는다
- 지수는 2^x에서 x를 의미합니다. 따라서 지수는 3입니다.
- 바이어스 지수로 계산해야 하므로 지수는 3+127(bias)입니다
- 130은 이진법으로 1000 0010(2)입니다
4. 가수(mantissa)를 찾는다
- 가수는 1.xxx에서 1 이하의 것들을 의미합니다.
- 즉, 가수부는 000 1010 0000 0000 0000 0000이 됩니다
5. 정답
|
0 |
1000 0010 |
000 1010 0000 0000 0000 0000 |
Ref
'Computer Science > 기초' 카테고리의 다른 글
| [DB] Database의 샤딩(Sharding) (0) | 2020.07.02 |
|---|---|
| 빅 엔디언 vs 리틀 엔디언 (0) | 2020.03.25 |
| HTTP Status Code (0) | 2019.11.13 |
- Total
- Today
- Yesterday
- nlp
- S3
- nlg
- Introduction to Algorithm
- 알고리즘
- AWS
- 알고리즘 강의
- 인공지능 스피커 호출
- aws cli
- TF2.0
- 6.006
- MIT
- netron
- Tensorflow2.0
- LSTM
- lambda
- 핵심어 검출
- tensorflow
- nlp 트렌드
- boto3
- BOJ
- 시계열
- stft
- wavenet
- RNN
- 모델 시각화
- MFCC
- 오디오 전처리
- librosa
- keras
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
