티스토리 뷰
[MIT_Introduction to Algorithm] 1강. 강의 소개 및 극댓값 찾기(Algorithmic thinking, peak finding)
JG Ahn 2019. 11. 28. 01:50Algorithmic thinking, peak finding
Intro & Algorithmic Thinking
이번 수업에서 1차원과 2차원 극댓값 찾기 문제 예시를 만나보고
이러한 극댓값 찾기 문제를 해결하는 알고리즘과 그 변형들을 알아볼 것입니다.
그러면 다양한 알고리즘 간의 차이점을 발견할 수 있을 텐데 이것을 복잡도 관점에서 살펴볼 것입니다.
다시 말해 이 알고리즘들이 각각의 효율성을 바탕으로 입력 크기에 따라 실행시간이 달라지는 것을 확인할 수 있습니다.
오늘 수업에서 비교적 간단한 알고리즘들을 점근적 복잡도 관점에서 분석해볼 것입니다.
알고리즘들을 비교해서 큰 입력이 있다고 가정했을 때,
이 알고리즘이 다른 알고리즘보다 점근적으로 복잡도가 더 낮으므로 더 빠르다고 판단할 수 있을 것입니다.
이 수업을 한 문장으로 요약하면 큰 입력을 받는 문제를 처리하기 위한 효율적인 방법에 관한 수업입니다.
큰 입력이란 미국 전역에 있는 모든 고속도로들의 지도인 미국의 고속도로 시스템이나
수억 개의 문자로 이루어진 사람 유전체, 또는 페이스북과 같이 500만 개 정도의 노드를 가진 사회 연결망 같은 것들입니다.
계산의 효율성은 중요하고 입력이 커질수록 더 중요해집니다.
십억 개의 요소를 몇 초 안에 읽을 수 있다고 가정해봅시다.
만약 알고리즘이 3차 복잡도를 가진다면 10의 9 제곱이 아니라 10의 27 제곱을 다루어야 합니다.
현대의 컴퓨터 조차 이렇게 큰 수는 처리하지 못합니다.
그래서 이 수업에서 우리의 관심사는 큰 규모의 문제를 다루는 효율적인 방법입니다.
또한 알고리즘의 확장성이 중요합니다
입력이 커짐에 따라 알고리즘이 어떻게 진행될지 추적할 수 있어야 합니다
크다는 것의 정의는 시간에 따라 변해왔는데 현재는 1조쯤 일 것입니다.
교수님이 대학생일 때는 1000 정도가 큰 것이었고 앞으로는 1조가 작은 수가 되어있을 수도 있습니다.
그러면 10의 18 제곱이 우리가 흔히 다루는 보통 크기의 입력으로 논의될지도 모릅니다.
Peak Finding
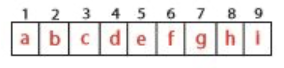
1차원에서의 극댓값 찾기는 숫자 배열에서 실행됩니다.
a~i는 숫자를 나타내고 음수, 양수 모두 가능합니다. 여기서는 모두 양수라고 가정하겠습니다.
문제는 여기서 극댓값을 찾는 것입니다.
그러려면 극댓값의 의미를 먼저 정의해야 하는데요
예를 들어, 2번 자리가 극댓값이라는 것은 b>=a 동시에 b>=c라는 의미입니다.
즉 극댓값이라는 것은 지역적인 특성입니다. (우리가 일반적으로 생각하는 1차원 배열에서 가장 큰 값을 찾는 문제가 아닙니다!)
1차원 문제에서는 매우 간단합니다.
왼쪽 값을 보고 오른쪽 값을 본 후 양쪽 요소의 값보다 크거나 같으면 현재 위치가 극댓값이 됩니다.
가장자리의 경우에는 한쪽만 확인하면 됩니다.
만약 i>=h 이면 9번 자리가 극댓값입니다.
1차원에서의 문제는 극댓값이 존재할 경우 그 값을 찾으라는 것입니다.
간단한 알고리즘으로는 배열을 따라가는 방법을 생각해볼 수 있습니다.
시작점을 왼쪽에서 시작하여 한 번 가로지른다고 합시다.
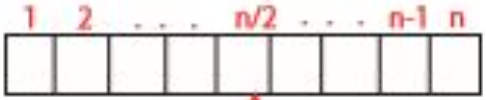
왼쪽부터 1, 2 그리고 중간 지점 n/2가 있는 원소가 n개인 배열입니다. 마지막에는 n-1과 n이 있죠
이렇게 표시하는 이유는 간단한 알고리즘을 찾는 것뿐만 아니라 알고리즘 복잡도와 입력의 개수 n의 관계를 정확하게 표현하기 위함입니다.
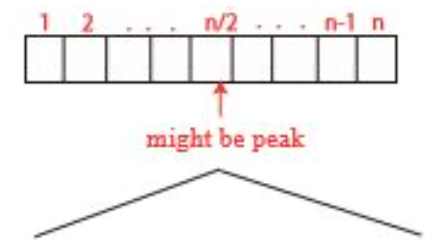
이것은 왼쪽에서 시작해서 오른쪽으로 걸어가는 알고리즘입니다.
즉 왼쪽에서부터 숫자가 증가하다가 중간 어딘가에 극댓값이 있고
그 이후로는 감소하기 시작하는 경우입니다. 이 경우에는 n/2가 극댓값입니다.
극댓값이 가장 오른쪽에 위치하는 상황도 있을 것입니다.
그러면 극댓값을 찾기 위해 오른쪽으로 이동하면서 총 n개의 원소를 확인하게 됩니다.
아까와 같이 극댓값이 중간에 위치한 경우에는 n/2개의 원소를 확인하면 됩니다
정중앙에 위치한 경우 말입니다.
최악의 경우의 복잡도는 Θ(n)이라고 표기합니다.
이 문제에서 최악의 경우는 n개의 원소를 모두 확인해야 하는 경우
즉 왼쪽 끝에서 시작해서 오른쪽 끝까지 가야 하는 경우입니다.
Θ(n)은 기본적으로 n의 차수에 대한 표현입니다.
따라서 상한 과 하한을 모두 나타내는데
O(n)은 상한을 의미합니다
다시 말하면 왼쪽에서 출발하는 이 알고리즘이 최악의 경우에는 n의 상수 배만큼의 복잡도를 갖는다는 것입니다.
따라서 이 알고리즘의 점근적 복잡도는 선형적입니다.
1차원 극댓값 찾기에서 알고리즘의 점근적 복잡도를 어떻게 낮출 수 있을까요? 이진 탐색 방식을 이용할 수 있습니다.
중앙에 있는 값보다 좌우에 더 높은 값이 있으면 그쪽에 극댓값이 있을 테니 절반을 잘라냅니다.
예를 들어 오른쪽 숫자가 더 크다면 오른쪽 절반 중 어딘가에 극댓값이 존재한다는 것이므로 그 부분만 확인하면 됩니다.
이런 식으로 절반씩 잘라나갑니다.
분할 정복을 이용하여 이 1차원 배열을 여러 개의 작은 배열들로 재귀적으로 쪼개는 것입니다.
이것을 반복하면 복잡도를 낮출 수 있습니다.
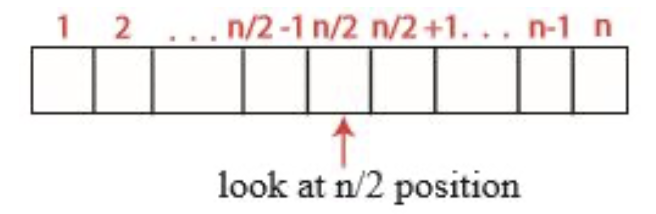
이 그림을 머릿속에 새겨야 합니다.
이것은 분할 정복 알고리즘입니다. 6.006 수업에서 이 패러다임을 계속해서 보게 될 것입니다.
먼저 n/2 위치를 봅니다. 그러고 나서 왼쪽을 보고 오른쪽을 봅니다
오른쪽을 먼저 보든 왼쪽을 먼저 보든 상관없습니다.
여기서는 왼쪽 절반을 먼저 보겠습니다.
만약 a[n/2] < a[n/2-1]이면 왼쪽 절반만 봅니다
1부터 n/2-1 까지만 보고 극댓값을 찾습니다.
a[n/2] < a[n/2-1]라는 조건이 만족되면 왼쪽으로 옮겨가서 문제의 절반만 해결하면 됩니다.
만약 이 조건이 만족되지 않고 a[n/2] < a[n/2+1] 라면
n/2+1부터 n까지에서 극댓값을 찾으면 됩니다.
왼쪽에서 했던 것과 마찬가지로 오른쪽 절반을 보면 됩니다.
만약 그게 아니라 이 두 조건이 모두 만족되지 않는다면 이미 극댓값을 찾은 겁니다.
이것이 가장 빨리 끝나는 최선의 경우이죠. n/2 위치가 바로 극댓값이기 때문입니다.
n/2 위치가 양 옆에 인접한 위치들보다 크거나 같다는 것인데 이게 바로 극댓값의 정의입니다.
이 재귀적, 분할 정복 알고리즘에 대응하는 T(n)의 점화식을 세워보세요.
그것을 이용하여 실제 복잡도를 Θ에 관하여 나타내려고 합니다.
- 최악의 경우는 T(n)이 상수의 시간이 되는 것인데요, 특정 원소를 확인하고 거기에 T[n/2]만큼 더해집니다.
이 알고리즘을 보고 계산량의 관점에서 알고리즘의 실행 시간에 관한 식을 세우라는 문제입니다.
T(n)은 크기가 n인 입력을 받았을 때 이 알고리즘이 하는 일의 양입니다.
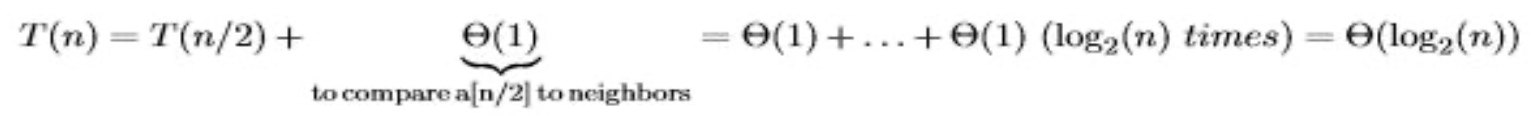
그러면 식을 이렇게 쓸 수 있습니다.
Θ(1)에 해당하는 것은 왼쪽과 오른쪽을 확인하여 두 번의 비교 연산을 실행하는 시간입니다.
여기서 2는 상수이므로 Θ(1)이 된 것입니다.
이것을 전개해나가면 결국 T(1) = Θ(1)이라는 탈출 조건에 도달합니다.
원소가 한 개인 배열에서는 그 원소를 극댓값으로 반환하기 때문입니다.
이 식을 쭉 풀어보면
T(n) = Θ(1) + ... + Θ(1)가 되는데
총 log₂n번 더하는 것이 됩니다.
이것을 모두 더하면 Θ(log₂n)의 복잡도입니다.
이것을 첫 번째 방법과 비교해보면 지수적 차이로 매우 큰 차이입니다.
파이썬 코드로 알고리즘을 작성했을 때
첫 번째 방법은 13초 (n = 1000만) 즉 Θ(n)은 13초 이고
두 번째 방법은 0.001초가 걸립니다
따라서 Θ(n)과 Θ(log₂n)은 아주 큰 차이입니다
2ⁿ과 n의 차이와 같습니다
이처럼 큰 입력을 받는 경우에는 복잡도를 낮추는 것이 합리적이라는 것을 알 수 있습니다.
1차원은 간단한 문제이기 때문에 지금이 최선입니다.
2차원의 극댓값 찾기로 넘어가면 알고리즘이 복잡해지면서 문제가 더 흥미로워집니다.
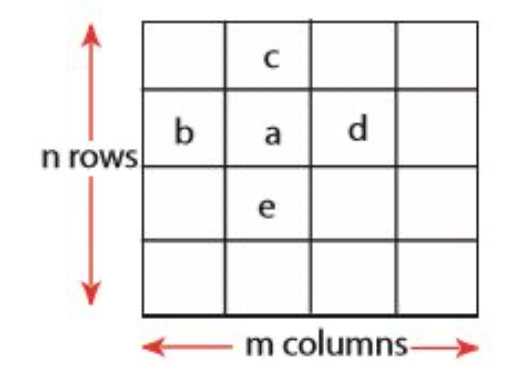
2차원에서는 행렬, 즉 2차원 배열을 다룹니다.
n개의 행과 m개의 열이 있다고 합시다
먼저 극댓값이 무엇인지 정의해야 합니다.
확실한 정의는 극댓값은 '언덕'입니다.
a, b, c, d, e가 위 그림과 같이 있을 때 a는 2차원 극댓값입니다.
a>=b, a>=c, a>=d, a>=e이라면 말이죠
즉 저 부분에 작은 언덕이 있는 겁니다.
여기서도 >=를 썼기 때문에 1차원과 마찬가지로 어떤 2차원 행렬에서든 극댓값이 존재합니다.
간단한 알고리즘을 보여줄 건데
탐욕 상승 알고리즘이라고 부르겠습니다.
탐욕 상승 알고리즘은 방향을 고르고 그 방향을 따라 극댓값을 찾습니다.
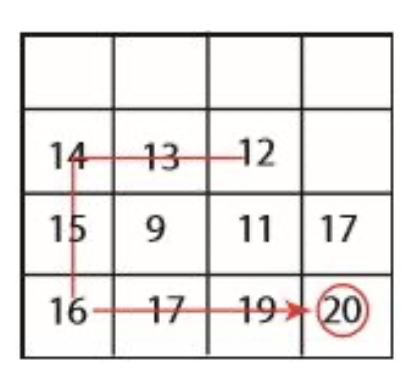
이런 행렬이 있다고 합시다.
탐욕 상승 알고리즘에서도 어디서 시작할지를 정해야 하는데
중앙에서 시작해서 왼쪽으로만 계속 갈 수도 있고, 오른쪽으로만 계속 갈 수도 있습니다.
그러다가 가장자리에 도착하면 아래로 내려갈 수도 있겠죠
이런 식으로 기본 탐색 방향을 정해야 합니다.
예를 들어 12에서 시작하여 왼쪽부터 본다고 합시다.
그 값이 더 크면 그 방향을 따라가고 그 값이 더 작으면 반대 방향으로 갑니다.
이 경우에는 12,13,14,15,16,17,10,20 이 순서대로 가서 극댓값을 찾을 것입니다.
1차원 경우와 마찬가지로 최악의 경우라면 주어진 행렬에 대해 시작 지점에 상관없이
왼쪽부터 보든 오른쪽부터 보든 또는 아래부터 보든 위부터 보든 전략에 상관없이 1차원에서 했던 것처럼
이 2차원 배열의 많은 원소들을 거쳐가야 하는 상황일 것입니다.
이러한 특정 시작 시점과 탐색 방향에 대한 이 알고리즘의 최악의 경우를 살펴보면
탐욕 상승 알고리즘은 Θ(nm)의 복잡도를 가집니다
n=m인 경우 라면 Θ(n²)의 복잡도를 가집니다
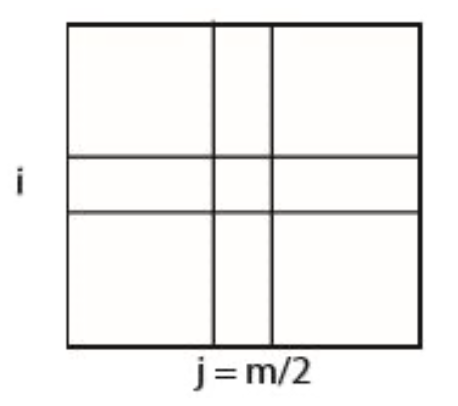
이진 탐색 알고리즘을 2차원에 집어넣는다고 생각해봅시다.
우선 할 것은 j=m/2인 중앙 열을 선택하여 어떤 알고리즘으로든 1차원 극댓값을 찾는 것입니다.
(i, j) 위치에서 극댓값을 찾았다고 합시다. 하나의 열을 골랐기 때문에 1차원 극댓값입니다.
이제 (i, j)가 시작 지점입니다.
i행에서 시작하여 i행의 1차원 극댓값을 찾는 것입니다.
이것은 아주 행복한 결과입니다
왜냐하면 중앙 열을 골라서 1차원 극댓값을 찾는 것은 Θ(log₂n) 복잡도입니다.
이걸 한번 수행하면 i행의 1차원 극댓값을 찾을 수 있습니다.
이 경우 i행은 길이가 m이므로 복잡도가 log₂m입니다. 만약 n=m이면 log₂n을 두 번 하는 것이 됩니다.
정말 끝일까요? 아닙니다
i 행에서 극댓값을 찾을 때 열 극댓값이 없을 수도 있습니다.
이 알고리즘은 정확하지 않습니다. 제대로 작동하지 않죠
효율적이지만 틀렸습니다. 알고리즘은 정확해야 합니다
정확하고 비효율적인 것이 부정확하고 효율적인 것보다 무조건 낫습니다.
이 알고리즘이 작동하지 않는 간단한 예를 들어보겠습니다.
문제는 2차원 극댓값이 i행에 존재하지 않을 수도 있다는 것입니다.
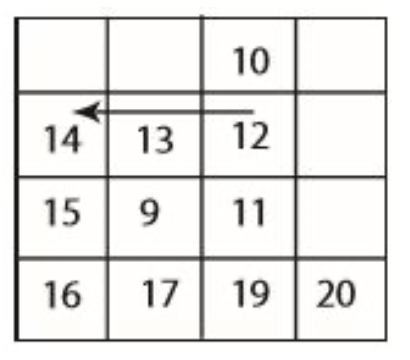
이것이 그 예시입니다. 우선 중앙 열에서 극댓값을 찾는데 중앙 열을 세 번째 열이라고 하겠습니다.
세 번째 열에서 극댓값은 12가 될 것입니다. (영상에서는 행이라고 하지만 앞의 내용과 문맥상 열이 맞는 것 같음)
19가 더 큰 수임에도 불구하고 10과 11 사이에서 12가 극댓값이기 때문입니다.
(극댓값은 지역적이고 양옆에 있는 값보다 더 큰 값이다. 순서상 19보다 12를 먼저 검증하기 때문에 19가 아닌 12가 극댓값이 될 것이다)
12가 있는 행을 골랐을 때 14를 극댓값으로 찾을 것입니다.
이 행에서의 1차원 극댓값이지요.
하지만 14는 2차원 극댓값은 아닙니다.
즉 이 예시에서 14를 극댓값으로 반환하지만 14는 2차원 극댓값이 아닙니다.
따라서 좋은 알고리즘이 아닙니다.
효율적인 알고리즘처럼 보이지만 제대로 작동을 안 합니다.
그러면 실제로 작동하는 알고리즘은 무엇일까요?
이것은 재귀의 경우인데 복잡도의 관점에서 탐욕 상승 알고리즘보다 효율적입니다.
그리고 이 알고리즘은 제대로 작동합니다.
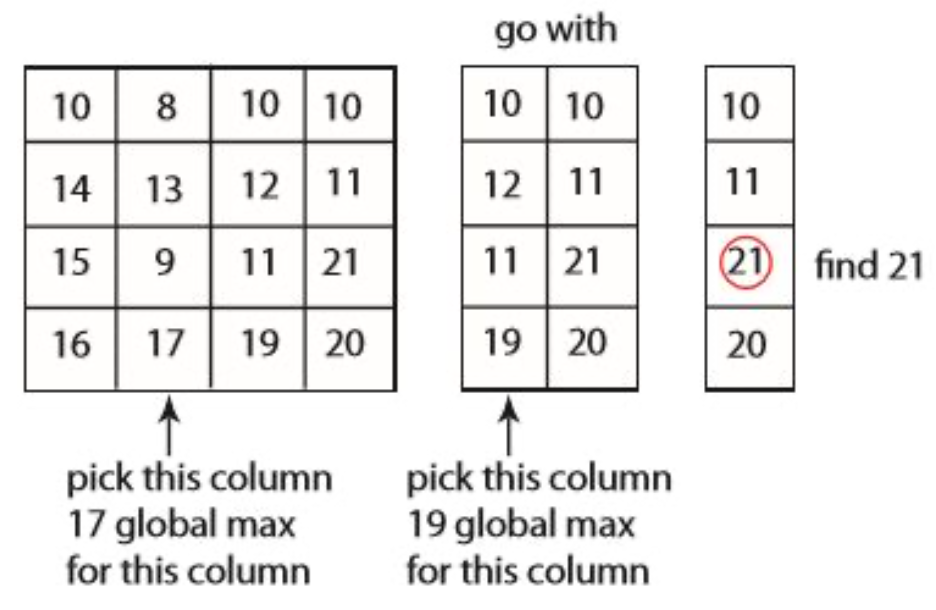
먼저 중앙 열을 선택합니다. 아까와 같이j=m/2입니다.
그다음 j열에서 최댓값을 찾습니다. 그것이 (i, j)입니다. (최댓값은 흔히 생각하는 최댓값이 맞습니다. 문제에서 구하던 극댓값이 아닙니다)
(i, j-1), (i, j), (i, j+1)을 비교합니다.
즉 최댓값을 찾고 나면 해당 행에서 왼쪽과 오른쪽을 보고 비교하기만 하면 됩니다.
만약 (i, j-1) > (i, j)이면 왼쪽 열을 고릅니다. 오른쪽도 마찬가지입니다.
만약 두 조건 모두 만족하지 않고 (i, j)가 (i, j-1)과 (i, j+1) 보다 크거나 같다면 끝난 겁니다. 1차원에서와 같이 말입니다.
만약(i, j) >= (i, j-1)이고 (i, j) >= (i, j+1)이면
그 말은 (i, j)가 2차원 극댓값이라는 것입니다.
그 이유는 (i, j)가 그 열에서 최댓값이었기 때문입니다.
해당 열에서 위 아래로 인접한 원소들과 비교한 결과 (I, j)가 최대였고
이제 왼쪽과 오른쪽을 봤더니 양쪽 원소보다 크거나 같다는 것을 발견했습니다.
따라서 그것이 2차원 극댓값입니다.
이 경우 왼쪽 또는 오른쪽 열을 고르면 열 개수가 절반으로 줄어든 채로 새로운 문제를 푸는 것과 같이 됩니다.
또한 1차원의 경우처럼 2차원 극댓값을 바로 찾고 끝내버리는 조건이 있습니다.
열이 1개인 경우에는 전체에서 최댓값을 찾으면 끝납니다. 이것이 탈출 조건입니다.

마지막으로 복잡도의 점화식을 써보고 이 알고리즘의 전체 복잡도를 구하겠습니다.
종합해보면 T(n, m) = T(n, m/2) + Θ(n)입니다.
n은 행 개수이고 m은 열 개수입니다.
한 번에 열 개수를 절반으로 쪼개서 m/2로 만들 것입니다.
그리고 최댓값을 찾기 위해서는 Θ(n) 만큼의 일을 수행해야 합니다.
한 번 쭉 훑어야 하니까요.
이런 식으로 쭉 가다가 T(n,1)=Θ(n)가 탈출 조건입니다
아까 한 것의 마지막 파트였죠.
T(n, m) = Θ(n) + ... + Θ(n), Θ(n)이 log₂m번 더해집니다
즉 Θ(nlog₂m)입니다
아직 극댓값 찾기가 끝난 것은 아닙니다.
파이썬으로 작성된 4개의 알고리즘을 볼 텐데 무슨 알고리즘인지는 알려주지 않을 것입니다.
여러분이 알아내야 합니다. 비슷한 것들을 이미 강의에서 보았을 것입니다.
여러분이 해야 할 일은 전에 말했던 것처럼 알고리즘을 분석하고 그중 맞는 것을 증명하고
맞지 않는 것에 대해서는 반례를 찾아야 합니다.
Q. 극댓값은 항상 존재하는데 문제에서 '존재할 경우'라는 말이 왜 들어가나요?
극댓값의 정의를 보면 크거나 같다는 조건이 있습니다.
만약 크거나 같다가 아니라 크다는 조건이었다면 그것이 성립하지 않습니다.
이 경우에는 문제 진술을 바꿔도 극댓값을 찾는 데에 지장이 없지만 만약 극댓값의 정의가 달랐다면 어땠을까요?
이것도 알고리즘적 사고의 일환입니다.
문제의 정의가 달라진다 해도 변형된 문제 또한 공략할 수 있는 보편적인 알고리즘을 만들고자 하는 것입니다.
Ref
[MIT] 파이썬을 이용한 알고리즘의 이해 : https://www.edwith.org/introalgorithm
MIT 6.006 Introduction to Algorithms : https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-006-introduction-to-algorithms-fall-2011/index.htm
'Memo > Things' 카테고리의 다른 글
| Conda 주요 명령어 정리 (0) | 2020.06.16 |
|---|---|
| [SNU_인공지능의 기초] 1강. 인공지능 소개 및 역사 (0) | 2019.12.06 |
| [SNU_K-MOOC]인공지능의 기초 강의 소개 (0) | 2019.12.05 |
| [MIT_Introduction to Algorithm] 2강. 계산 모델과 문서 거리(Models of computation, document distance) (0) | 2019.11.29 |
| [MIT_edwith] 파이썬을 이용한 알고리즘의 이해 강좌 소개 (0) | 2019.11.27 |
- Total
- Today
- Yesterday
- 핵심어 검출
- BOJ
- netron
- 알고리즘
- TF2.0
- 인공지능 스피커 호출
- Tensorflow2.0
- keras
- 모델 시각화
- S3
- nlp
- Introduction to Algorithm
- 알고리즘 강의
- lambda
- stft
- wavenet
- nlg
- 오디오 전처리
- 시계열
- boto3
- RNN
- librosa
- aws cli
- MIT
- LSTM
- tensorflow
- AWS
- MFCC
- nlp 트렌드
- 6.006
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
