티스토리 뷰
회귀의 평가를 위한 지표는 실제 값과 회귀 예측값의 차이를 기반으로 합니다. 회귀 평가지표 중에 RMSLE가 있는데 값이 작을수록 회귀 성능이 좋은 것입니다. 예측값과 실제값의 차이가 없다는 뜻이기 때문입니다.
$$RMSLE = \sqrt{\frac{1}{N}\sum_{i=1}^{N}{(\log(p_i+1)-\log(a_i+1))^2}}$$
$$p=Predicted, \: a=Actual$$
RMSLE는 위와 같은 식을 가지는데 RMSE와 비교해 3가지의 차이점을 보입니다.
RMSE와 비교해 RMSLE의 3가지 장점
1. 아웃라이어에 강건해진다
RMSLE는 아웃라이어에 강건(Robust)합니다.
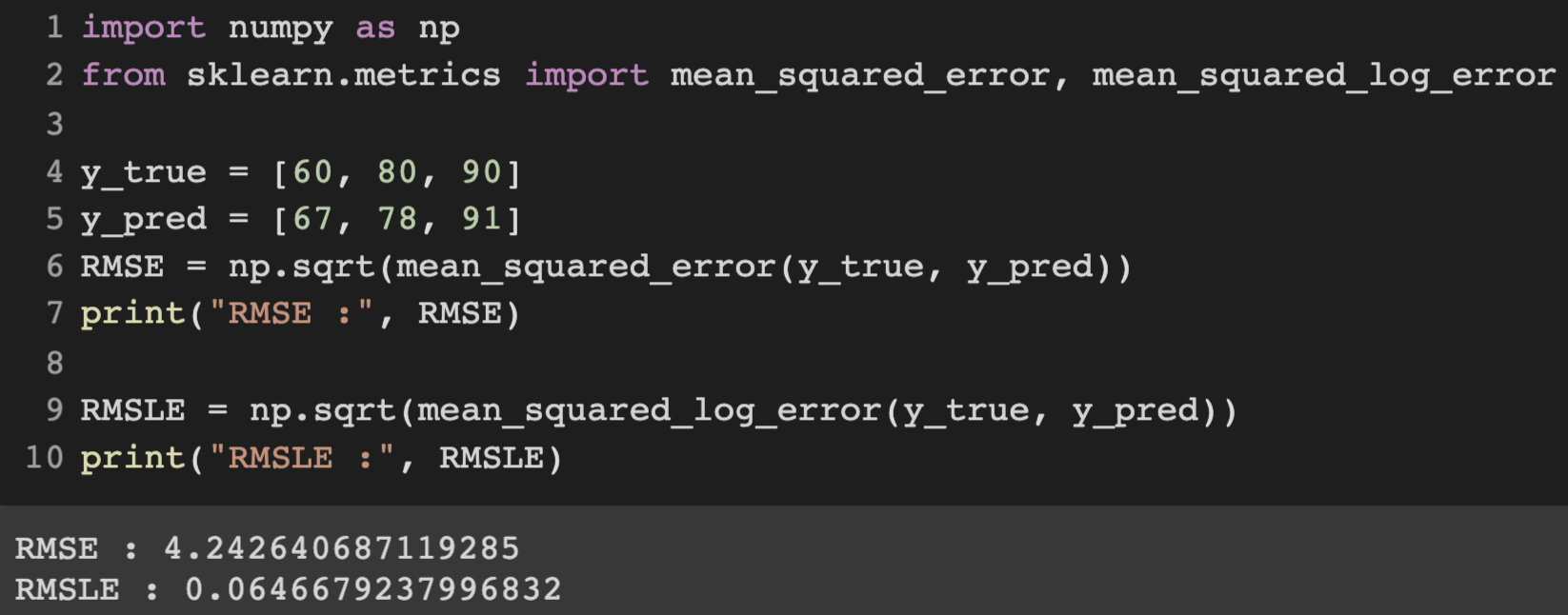

실제값 = [60, 80, 90], 예측값 = [67, 78, 91] 일 때, RMSE = 4.242, RMSLE = 0.6466이고
실제값 = [60, 80, 90, 750], 예측값 = [67. 78. 91. 102] 일 때, RMSE = 324.02, RMSLE = 0.994입니다.
750이라는 아웃라이어 때문에 RMSE는 굉장히 증가했지만 RMSLE의 증가는 미미합니다.
RMSLE는 아웃라이어가 있더라도 값의 변동폭이 크지 않습니다. 따라서 RMSLE는 아웃라이어에 강건하다고 말할 수 있습니다.
2. 상대적 Error를 측정해준다.
예측값과 실제값에 로그를 취해주면 로그 공식에 의해 아래와 같이 상대적 비율을 구할 수 있습니다.
$$\log(p_i+1)-log(a_i+1)=\log(\frac{p_i+1}{a_i+1})$$

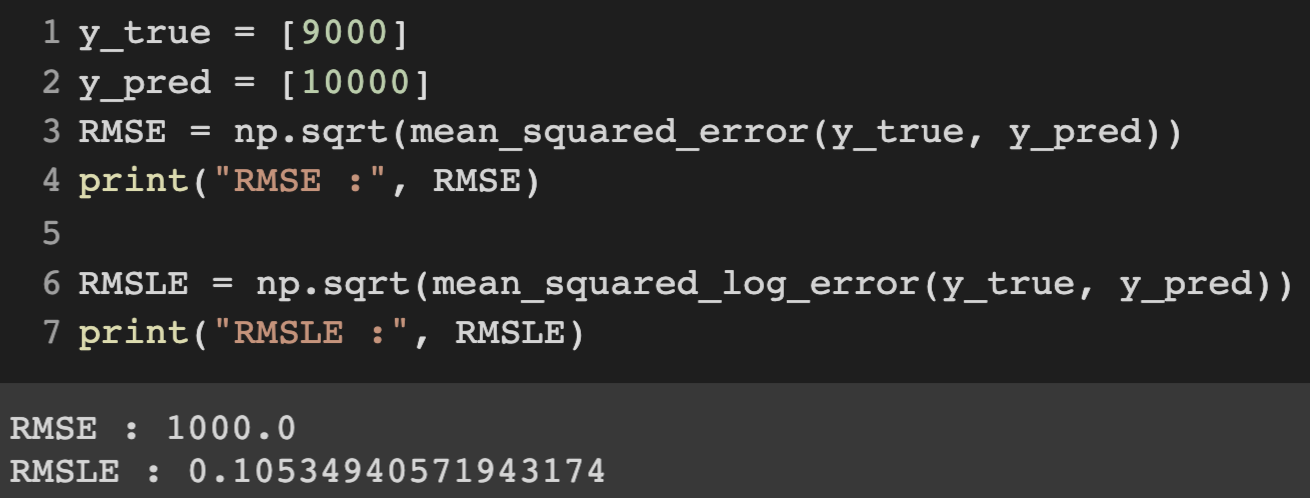
위의 코드를 보면 값의 절대적 크기가 변하더라도 상대적 크기가 동일하다면 RMSE값은 변합니다. 따라서 RMSE와 달리 RMSLE는 예측값과 실제값의 상대적 Error를 측정해줍니다.
Ref [RMSLE의 한계]라는 글을 보시면 RMSLE의 상대적 Error 측정이 오히려 독이 되는 경우를 확인하실 수 있습니다.
금전적인 부분을 예측하는 문제인데, RMSLE의 특성 때문에 큰 금액을 비슷하게 예측하는 것보다 적은 금액을 큰 차이 없이 예측하는 것이 더 좋게 나옵니다.
1억을 100억으로 잘못 예측하면 절대적으로는 99억이 차이나지만 error는 \(\log(10000000000+1)-\log(100000000+1) = \log(100)\)입니다.
0원을 99원으로 잘못 예측하면 99원이 차이나지만 error는 \(\log(99+1)-\log(0+1) = \log(100)\)입니다.
위의 계산 결과를 보면 1억과 100억의 error가 0원과 99원의 error와 같다는 것을 알 수 있습니다.
상대적인 Error를 측정해주는 것이 장점도 있겠지만 이렇게 금전적인 부분의 Error 계산에선 좋지 않을 수도 있겠다는 생각이 듭니다.
3. Under Estimation에 큰 페널티를 부여한다.
RMSLE는 Over Estimation보다 Under Estimation에 더 큰 페널티를 부여합니다. 즉 예측값이 실제값보다 클 때보다 예측값이 실제보다 작을 때 더 큰 페널티를 부여합니다.


위의 코드와 같이 예측값과 실제값의 차이는 둘 다 400입니다. Over Estimation이든 Under Estimation이든 RMSE 값은 동일합니다. 하지만 RMSLE는 Under Estimation일 때 (즉 , 예측값이 실제값보다 작을 때) 더 높은 페널티가 주어집니다.
배달 음식을 시킬 때 30분이 걸린다고 했는데 실제로 20분이 걸리는 건 큰 문제가 되지 않지만, 20분이 걸린다고 했는데 30분이 걸리면 고객이 화가 날 수가 있습니다. 이럴 때 RMSLE를 적용할 수 있습니다.
Ref
'Machine Learning > Basics' 카테고리의 다른 글
| 머신러닝 용어 정리 (0) | 2020.07.18 |
|---|---|
| sparse_categorical_crossentropy와 categorical_crossentropy 비교 (0) | 2020.07.11 |
- Total
- Today
- Yesterday
- aws cli
- nlg
- tensorflow
- BOJ
- MFCC
- S3
- MIT
- nlp
- 핵심어 검출
- RNN
- Introduction to Algorithm
- 6.006
- 알고리즘
- keras
- wavenet
- 모델 시각화
- 오디오 전처리
- 인공지능 스피커 호출
- lambda
- LSTM
- librosa
- TF2.0
- stft
- 알고리즘 강의
- Tensorflow2.0
- netron
- 시계열
- nlp 트렌드
- AWS
- boto3
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
