티스토리 뷰
본 게시글은 [라온 피플] CNN구조 3 - VGGNet, ResNet 글을 정리한 것입니다.
VGGNet
2014년 ILSVRC에서 GoogleNet과 함께 주목을 받았고 간소한 차이로 2위를 차지했지만 VGGNet은 간단한 구조와 단일 network에서 좋은 성능 등을 보여준다는 이유로, 1위를 차지한 GoogleNet보다 많은 network에서 응용되고 있다.
VGGNet은 사실 network의 깊이(depth)가 어떤 영향을 주는지 연구하기 위해 설계된 network이다.
그래서 convolution kernel 사이즈를 한 사이즈로 정하고 Convolution의 개수를 늘리는 방식으로 테스트를 진행합니다.
Convolution Layer는 kernel 사이즈 3x3, padding 사이즈 1로 설정해서 convolution layer를 통해서 이미지 resize를 한 것이 아니라 max pooling을 사용해서 이미지 resize를 합니다.
Max pooling은 kernel 사이즈 2x2, stride 2로 이미지를 절반으로 resize 합니다.
아래 그림은 VGGNet이 layer의 깊이를 어떻게 늘려가며 테스트했는지 보여줍니다.
Network는 convolution layer를 추가함으로써 깊이가 깊어지는 것을 볼 수 있습니다.

이론적으로 보면 5x5 kernel이나 3x3 kernel을 2개 사용하는 거나 성능적으로는 동일할 것입니다.
하지만 VGGNet팀이 테스트한 결과 3x3 kernel을 중첩해서 사용하는 게 성능은 더 좋다고 합니다.
그 이유는 non-linear 함수 ReLU가 더 많이 들어가서, decision function이 더 잘 학습된다고 볼 수 있습니다.
또 한 가지 이유는 학습을 해야 할 parameter 수가 줄어듭니다.
그러므로 큰 사이즈의 kernel보다는 작은 사이즈 kernel을 중첩해서 사용하는 게 성능도 더 좋고, 학습할 parameter도 더 적어서 속도도 더 빨라집니다.
VGGNet의 구조는 간단하지만 최종단에 fully-connected layer 3개를 붙여서 parameter수가 너무 많다는 단점이 있습니다.
최종단 fully-connected layer에만 parameter개수가 약 122 million 개나 됩니다.

VGGNet의 깊이에 따른 오차를 보면 network의 깊이가 깊어질수록 error가 내려가는 것을 볼 수 있습니다.
하지만 D(16-layer)와 E(19-layer)를 비교하면 error가 비슷하거나 더 나빠지는 걸 보실 수 있습니다.
그렇다면 19-layer보다 nerwork를 더 깊게 설계하면 어떻게 될까요? 이 테이블을 보면 결과는 더 나빠질 것이라고 추측할 수 있습니다.
일반적으로 모델의 깊이가 깊어질수록 성능이 좋아지지만 특정 깊이부터는 성능이 나빠진다는 것을 알 수 있습니다.
ResNet
VGGNet에서도 언급했지만 Deep Learning은 기본적으로 망이 깊어질수록 성능이 더 좋아진다고 생각합니다.
이전까지 설계된 deep learning network는 8-layer 수준이었고, VGGNet에서 19-Layer까지 테스트를 하였습니다.
하지만 VGGNet의 16-layer와 19-layer의 성능 차이는 거의 없었습니다.
만약 19-layer보다 더 망을 깊게 설계하면 어떻게 될까요?
Deep Network의 문제점
ResNet팀이 망이 깊어지는 경우 어떤 결과가 나오는지 실험을 하였습니다.
20-layer와 56-layer에 대해서 비교 테스트를 진행하였고, 결과는 아래 그림과 같습니다.

위 그림을 보면, 56-layer의 결과가 더 나쁘게 나오는 걸 확인할 수 있습니다.
다른 이미지 데이터를 사용하거나 layer 수를 변경을 해봐도 같은 결과가 나올 것입니다.
그 이유는 뭘까요?
망이 깊어지면 gradient vanishing/exploding 또는 degradation이 발생하게 됩니다.
하지만 ResNet은 망의 깊이를 처음에 152-layer까지 늘렸고, 후에는 망의 깊이는 1001-layer까지 늘려서 설계했습니다.
ResNet의 구조
아래와 같은 평범한 CNN 망을 살펴보겠습니다.
이 망은 입력 x를 받아 2개의 weighted layer를 거쳐 출력 H(x)를 내며, 다음 layer의 입력으로 적용됩니다.

ResNet은 layer의 입력을 layer의 출력에 바로 연결시키는 "skip connection"을 사용했습니다.
아래 그림은 ResNet 구조입니다.

출력이 H(x)가 F(x) + x로 변경이 되었습니다.
그림만으로 보면 단순히 weight layer를 통해 나온 결과와 그 전 결과를 더하고 relu를 사용한 것뿐인데, 그 성능은 대단하였습니다.
그 이유는 기존 network 들은 H(x)를 얻기 위한 학습을 했다면, ResNet은 F(x)가 0이 되는 방향으로 학습을 합니다.
F(x) = H(x) - x고, F(x)를 학습한다는 건 나머지(residual)를 학습한다고 볼 수 있고, 그렇기 때문에 ResNet이라 불리게 됩니다.
또한 x가 그대로 skip connection이 되기 때문에 연산 증가는 없고, F(x)가 몇 개의 layer를 포함하게 할지 선택이 가능하며
Fully-Connected layer 외에 Convolution Layer도 가능합니다.
그리고 x와 H(x)의 dimension이 다르면 dimension을 맞추기 위해 parameter w들을 추가해서 학습시킵니다.
테스트 Network 설계
ResNet 팀은 성능 비교를 위해 일반적인 Plain Network와 Residual Network을 설계하였고,
기본 틀은 VGGNet을 참고하였습니다. Plain Network와 Residual Network의 구조는 아래 그림과 같습니다.

Plain Network와 Residual Network는 아래와 같은 Network 특징을 가지고 있습니다.
- Convolution Layer는 3x3 kernel을 사용
- 복잡도를 줄이기 위해 max-pooling, hidden fc, dropout 등을 사용 안 함
- 출력 feature-map 크기가 같은 경우, 해당 모든 layer는 모두 동일한 수의 filter로 설정
- 출력 feature-map 크기가 절반이 될 때에는, layer의 연산량 보존을 위해 filter의 개수를 2배로 늘린다.
- 출력 feature-map 크기를 줄일 때는 pooling 대신에 convolution stride의 크기를 "2"로 설정
- Residual Network는 2개의 Convolution Layer마다 skip connection을 연결
실험 결과
아래 그림은 18-layer와 34-layer에 대한 Plain Network와 Residual Network의 실험 결과입니다.

Plain Network의 경우, Resnet 논문에서 언급하기를 BN을 적용해서 Forward Propagation 신호가 0이 아닌 걸 확인했고,
Backward Propagation의 Gradient 값들이 괜찮은 크기를 갖는 것을 확인했기 때문에 34-layer의 error가 18-layer 보다 큰 이유는 gradient vanishing으로 야기된 게 아닙니다.
Residual Network의 경우, 34-layer의 결과가 18-layer보다 좋다는 것을 그래프를 통해 알 수 있고, 수렴 또한 더 빨리 된다는 것을 알 수 있습니다.
개선된 ResNet 구조
2015년에 발표한 ResNet은 H(x) = ReLU(F(x) + x)의 수식을 가지고 있습니다.
ReLU라는 activation function에 의해 blocking이 일어나게 됩니다.
다음 layer로 보내는 출력이 앞 layer에서 입력으로 가져온 온전한 skip connection이 아닙니다.
이러한 문제로 인해 ResNet팀은 ReLU를 F(x) 안에 넣고,
H(x) = F(x) + x라는 온전한 skip connection block을 설계하게 됩니다.
수식으로 표현하면 아래 그림과 같습니다.

ResNet 팀은 Actication 함수의 위치가 어떤 영향을 주는지 확인을 하기 위해
다음 그림과 같은 다양한 조합의 F(x) block에 대하여 실험을 진행했습니다.

- (b)는 BN의 위치를 addition 뒤로 옮김.
- 결과적으로 BN이 Propagation path를 방해할 수 있으며, Origin보다 결과가 좋지 못하다.
- (c)는 addition 뒤에 있는 ReLU를 residual net 쪽으로 옮김.
- 원래 Residual 함수가 (-∞, +∞) 범위인데, ReLU 때문에 결과가 non-negative가 나와서 representation 능력이 떨어지고 성능도 나빠진다.
- (d)와 (e)는 pre-actiation 성능을 확인하기 위한 구조.
- ReLU가 진정한 identity mapping 개념을 방해하기 때문에 이것을 움직이기 위한 테스트.
Why ResNet Worked?
왜 ResNet은 깊은 network에서도 학습이 되는지에 대해서 자세히 알아보겠습니다.
그전에 gradient vanishing 이 왜 발생하게 되는지에 대해서 설명하겠습니다.

위 그림을 보시면 back Propagation으로 weight를 갱신할 때, 앞쪽 Layer로 갈수록 weight가 작아지는 것을 볼 수 있습니다.
그럼 network가 깊어지면 weight가 계속 작아질 것이고 마지막에는 0으로 변해서 학습이 안 되는 현상이 발생합니다.

그럼 만약 ResNet과 같이 앞 layer를 skip connection으로 다음 layer에 연결하면 back propagation이 어떻게 변할까요?
그림의 주황색 선은 "Skip connection"입니다. 그림과 같이 Skip connection으로 gradient는 dh(x)/dx = 1이 됩니다.
previous layer에 최종 전달되는 gradient는 [0.0001, 0.01]에서 [1, 0.0001, 0.01]이 됩니다.
1이라는 gradient가 더 추가가 되어서 Previous layer에 전달이 됩니다.
이런 이론을 적용하면 Gradient Vanishing을 줄일 수 있겠지만 어디까지나 한 개의 module에 관해서만 가능합니다.
실제로 ResNet은 많은 Module을 사용하며, 이 방식이 아니더라도 BN, ReLU만으로도 어느 정도의 깊이의 network까지는 gradient vanishing 이 발생하지 않습니다.
Cornell 대학에서 발표한 논문 "Residual Networks Behave Like Ensembles on Relatively Shallow Networks"은 ResNet에 대해 재미있는 분석을 했습니다.
아래 그림은 ResNet의 skip connection이 어떻게 구성되어 있는지 보여줍니다.
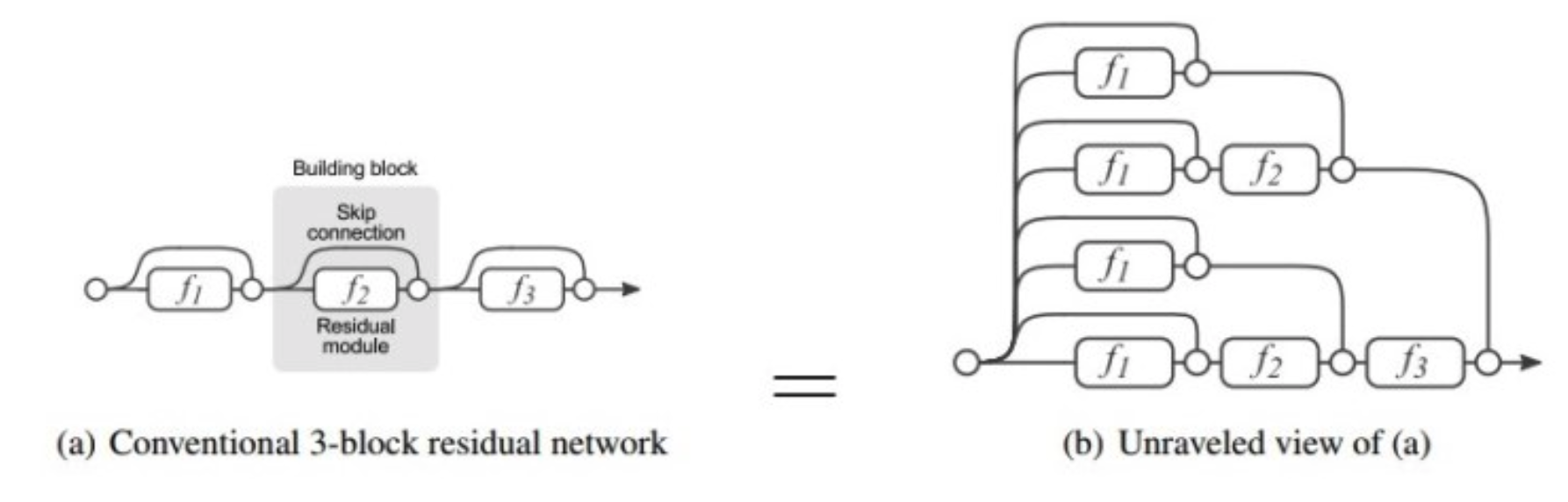
ResNet 이전 network (VGGNet, AlexNet 등)들의 각 Layer 입력은 그 전 layer의 출력에 의지하게 됩니다.
하지만 ResNet은 위 그림에 보시는 바와 같이 각 layer 입력은 다른 구조의 network의 출력이 됩니다.
그러므로 ResNet 이전의 network들은 각 layer의 path길이가 동일하지만, ResNet은 각 layer의 path 길이가 다릅니다.
논문에서는 몇 가지 실험을 진행하였습니다.
● Deleting individual layers from neural networks at test time
아래 이미지는 테스트 결과입니다.
VGGNet은 검사 자체가 안 되는 반면 ResNet은 어떠한 layer를 삭제한다고 해서 검사에 영향을 주지 않는 걸 보실 수 있습니다.
그러므로 ResNet은 각 layer가 독립적이라 볼 수 있으며, 상호 간의 의존하지 않는다고 볼 수 있다.

● Deleting many modules from residual networks at test-time
아래 그림을 보면 삭제한 Layer가 많을수록 error가 비례적으로 커지는 것을 볼 수 있습니다.
그 말은 ResNet은 Ensemble System이라는 의미라고 볼 수 있습니다.

● The Importance of short path in residual networks
앞에서 이미 ResNet은 서로 다른 path length를 가진 layer가 연결된 형태라고 설명하였습니다.
오직 1개의 path만 전체 module을 통과하고, n개의 Path는 1개의 module만 통과합니다.
이 이유 때문에 path길이는 이항 분포를 따르고, 아래 그림을 보면 path의 95% 이상이 19~35 module을 통과합니다.
그리고 (c)를 보면 실제로 path 길이가 길면 gradient vanishing 현상이 나타납니다.
그러므로 ResNet은 path 길이가 짧은 layer가 실제로 동작한다고 볼 수 있고, Gradient Vanishing 현상을 완전히 해결했다고 보기는 어렵습니다.
ResNet을 알기 위한 정말 다양한 연구가 있습니다. 그렇기 때문에 모든 걸 이 포스트에 담을 수는 없을 것 같습니다.
ResNet이 어떻게 학습이 되는가에 대해 질문을 하고, 개인적인 해답은 한 논문을 예제로 설명했습니다.
ResNet에 대해 저 자세히 알고 싶다면 [라온 피플] ResNet을 읽어보시길 추천드립니다.
- Total
- Today
- Yesterday
- Introduction to Algorithm
- TF2.0
- 인공지능 스피커 호출
- nlp 트렌드
- MIT
- librosa
- RNN
- lambda
- MFCC
- keras
- BOJ
- wavenet
- netron
- AWS
- 시계열
- 핵심어 검출
- 오디오 전처리
- stft
- 알고리즘
- LSTM
- aws cli
- nlg
- 6.006
- tensorflow
- S3
- nlp
- boto3
- 모델 시각화
- 알고리즘 강의
- Tensorflow2.0
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
